The Computational Media Lab at the ANU focus on computational problems for understanding online media and their interactions with and among humans. We develop core methods in machine learning and optimization. We also formulate and solve problems in understanding online behavior, multimedia and the broader implications of machine intelligence.
You may be interested in sampling the recent blog posts below, look at our research summary, publications, all past posts, or navigate by categories and tags.
Recent updates
See here for archived news items.Recent talks and video demos
Data-driven Understanding of 100,000 Everyday Moral Dilemmas Posted on Feb 13, 2024
We analysed the 7-year history of /r/AmITheAsshole, asked two questions and got two surprising answers.
Posted by Lexing Xie and Ziyu Chen.
Thanks to Eric Byler for a 2022 profile article in college news!
We identify Reddit’s Am I the Asshole (AITA) forum as a rich source of data to investigate the moral sphere using AI and machine learning. This work is done with Josh Nguyen and Alasdair Tran, and ANU philosophers Colin Klein, Nick Carroll, and most recently Nick Schuster.
Read MoreTransform and Tell: Entity-Aware News Image Captioning Posted on May 29, 2020
We develop a fully end-to-end news image captioning system that can generate entity names.
Posted by Alasdair Tran, with edits from Lexing Xie. Thanks to Ingrid Fadelli for sending us interview questions.
In our recent paper published in CVPR 2020, we propose an end-to-end model that can generate linguistically-rich captions for news images. We also build a live demo where people can generate a caption for any New York Times article.
Read MoreInfluence Flowers of Academic Entities Posted on Dec 31, 2019
We present a new interactive webapp for exploring the rich intellectual heritage of academic entities.
Posted by Minjeong Shin, with edits and additions by Lexing Xie

In our recent paper in IEEE VIS’19, we introduced a new visual metaphor, called the Influence Flowers to represent flow influence between academic entities including people, publication venues, institutions, and topics.
Read MoreAI and Cars - a Historical Analogy Posted on Jul 17, 2019
Three timelines in developing and adopting cars may shed light on what humanity would do with machine intelligence.
Posted by Lexing Xie. Thanks to Mario Günther, Ignacio Ojea Quintana, Swapnil Mishra and Atoosa Kasirzadeh for many great suggestions.
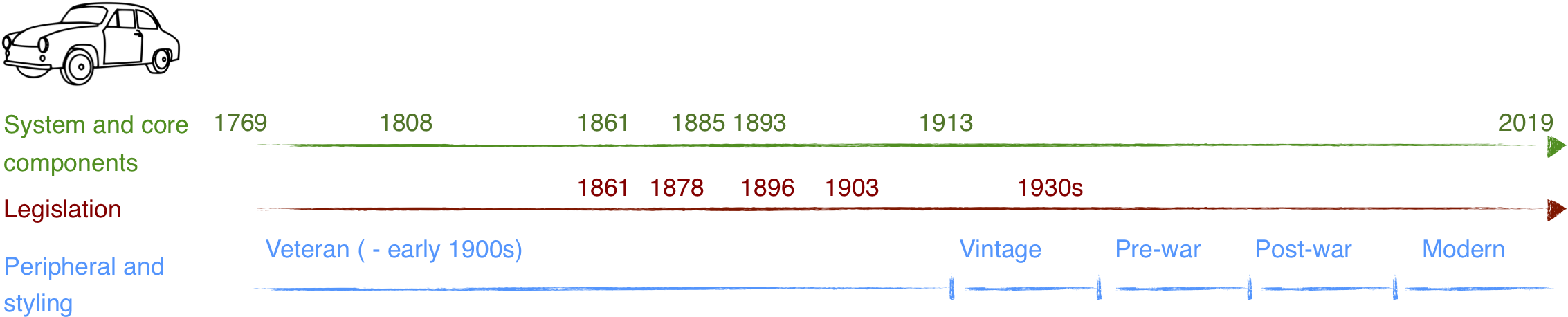
Fig. 1: Overview of three concurrently evolving timelines in the development of cars2. Top (green) - key events in engine and early system developments. Middle (red) - key events in car and road-safety related legislations. Bottom (blue) - rough separation of eras in car styling. Key events selected from Wikipedia narratives on cars and history of the automobile3. See article for discussion. For readability, time scales are not uniform.
Read MoreSemStyle: Learning to Caption Images like Romantic Novels Posted on Jun 10, 2018
A new machine learning system that styles your caption like master story-tellers do.
posted by Lexing Xie and Alex Mathews

The Layered Cake Structure of a Paper Posted on Mar 25, 2018
The craft of paper writing can be mastered using recipes.
posted by Lexing Xie, additions and edits by Aditya Menon
 I like cakes, and I enjoy reading logically lucid research articles.
This post argues that research papers can benefit from explicitly thinking about and planning its four logical layers, just like a multi-layered
Mille-feuille, or Napoleon cake (image credit: alyonascooking).
I like cakes, and I enjoy reading logically lucid research articles.
This post argues that research papers can benefit from explicitly thinking about and planning its four logical layers, just like a multi-layered
Mille-feuille, or Napoleon cake (image credit: alyonascooking).
Quick Planning with Action Schema Networks Posted on Feb 26, 2018
How tricks from computer vision and deep learning can be used to accelerate planning algorithms
posted by Sam Toyer and Sylvie Thiébaux

Planning algorithms try to find series of actions which enable an intelligent agent to achieve some goal.
Such algorithms are used everywhere from manufacturing to robotics to power distribution.
In our recent paper at AAAI ‘18, we showed how to use deep learning techniques from vision and natural language processing to teach a planning system to solve entire classes of sophisticated problems by training on a few simple examples.
Read MoreLife Outside of Research in 2017 Posted on Dec 21, 2017
Siqi and Alex received sports and community accolades, respectively. The lab enjoyed two outings in town.
posted by Quyu Kong, with edits from Lexing Xie
Sports is a prominent theme in Canberra. This post celebrates two of our competitive athletes, and looks back at two outings when the whole lab flexed our muscles and got a little bit wet.
Read MoreExpecting to be HIP (IV) - HIPsters Unite! Posted on Jul 24, 2017
The Hawkes Intensity Process (HIP) inspired a small cascade of puns, and a research-team-in-uniform
Expecting to be HIP (III) -- Examining the role of promotions Posted on Jun 12, 2017
How much promotion is required, and why should one constantly promote?
posted by Marian-Andrei Rizoiu , edited by Lexing Xie
“The fundamental scarcity in the modern world is the scarcity of attention.” – Herbert A. Simon.
Human attention is a limited resource and influencing the mechanisms governing its allocation is the holy grail of advertisement. Our ICWSM'17 paper applies the recent HIP popularity modeling to further examine popularity under promotion and answer questions such as:
- How much promotion is required for this item to rise to the top 5% in popularity?
- How fast will an item respond to a given amount of promotion?
- Why is constant promotion desirable?
to be HIP (II) -- Could this video go viral? Posted on Jun 11, 2017
supplying the missing link between popularity and promotions
posted by Marian-Andrei Rizoiu , edited by Lexing Xie
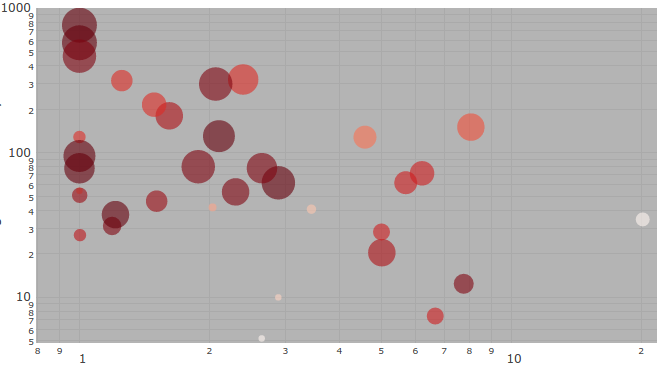
One major gap in understanding social media is to precisely quantify the relationship between the popularity of an online item and the external promotions it receives. Our recent WWW'17 paper supplies the missing link. We use a mathematical model to describe the continuous interaction between external promotions (e.g. tweets about a video) and popularity dynamics (e.g. daily views). This in turn answers several practical questions:
- Can we explain the complex multi-phased popularity dynamics widely seen online?
- Can one predict what could become viral?
- Can one predict what would not become viral even if heavily promoted?
Escape from broadcasting: Talk shows as news sources Posted on May 26, 2017
We analyze news sources on YouTube to reveal their roles in broadcasting information.
posted by Siqi Wu, edited by Marian-Andrei Rizoiu and Lexing Xie

We are in an era when information consumption and production are democratized. Regular users not only consume information, but they digest, mutate and produce new information which gets passed on to other users. Prompted by a press inquiry from the Polish online news www.press.pl, we analyze the impact of these emergent sources of information versus traditional media, in the context of politics. More precisely, we study how YouTube videos posted by two traditional news sources (BBC news/UK, ABC news/USA) and two emergent online news sources (The Alex Jones Channel, The Young Turks) are viewed around the time of the US political elections of 2016.
Read MoreTags and Categories
Problems
social media popularity privacy language vision citationsMethods
deep learning stochastic process visualizationMeta
research data code datasci news group-activityGetting in touch:
Drop us a line if you are interested in knowing more about our work, collaborating, or joining us.
The humanising machine intelligence project is recruiting two research fellows, see here.
We are not actively recruiting PhDs for 2021-2022, but if you have a strong track record and believe your interests and ours are a tight fit, feel free to drop us a line with your CV.
